수강 일자: 07월 20일
머신러닝 공부는 이론보다는 프로젝트를 통해서 코딩하는 법을 익히는 것이 중요하다고 합니다.
하지만, 가장 기본적인 classification 도 남들이 만들어 놓은 결과를 그대로 가져다 쓸 뿐입니다.
예를 들어 , softmax는 Label 수만큼의 결과를 가지고 있고 , 더한 값은 1이 되는 확률 값입니다.
*그냥 그렇다고 넘어가고 , 자세히 설명해주진 않습니다. *
인공지능 , 특히 딥러닝 알고리즘에서 특징을 추출한 다음에 결과 도출은 확률론에서 나온 이론을 사용합니다.
이번 확률론을 공부하면서 인공지능에서 Black Box로 여기던 부분을 더 파헤쳐 보겠습니다
Statistics 110 1강입니다.
확률론의 활용영역:
- 유전학, 물리학, 계랑 경제학, 금융, 역사학, 정치
- 인문학, 사회과학계에서도 중요도와 활용이 늘어나고 있음
- 도박과 게임 - 통계에서 여러 번 연구된 주제이다(페르마, 파스칼)
- 인생 전반: (수학이 확실성에 대한 학문이라면,) 확률은 불확실성(uncertainty)을 계량화하는 것을 가능하게 해 준다.
확률론은 응용 분야가 점점 더 늘어나고 있습니다.
확률론에 임할 때 명심할 것이 있습니다.
그건 바로 직관에 의존하지 않는 것입니다.
이전에는 사람들이 단순히 확률의 문제를 직관적으로 써 내려가면서 해결하려고 했습니다.
유사점을 찾아내서 다양한 발견법을 만들어냈었죠.
불행히도, 대부분의 발견법은 결과적으로 틀린 것임을 알게 되었습니다.
뉴튼도 예전에 주사위 도박 문제를 정확하게 계산했었습니다. 하지만
그의 직관은 결과적으로 틀린 것이 되었습니다.
우리가 하는 거의 모든 것들이 굉장하게 직관에 어긋나 있습니다.
이것이 이 통계학이 굉장히 흥미로운 이유인 것 같습니다.
이제 본격적인 내용으로 넘어가도록 하겠습니다.
확률은 그동안 점성술과 같은 것으로 생각했습니다.
확률을 수학적 발견으로 생각하게 해 준 엄청난 발견이 있었다.
바로 , 집합(set)이다.
그리고 , 몇 가지 정의를 하겠습니다.
표본 공간(sample space): set of possible outcomes of experiment (실험의 모든 가능한 결과의 집합)
Experiment: 실험 은 어떤 것이든 될 수 있다.
무엇이든지 하면 거기에 특정한 결과가 있고 , 실행하기 전에 알 수 없다.
여러 가지 가능한 결과가 있기 때문이다. 어떤 결과가 될지 알 수 없다.
Event(사건): subset of sample space(표본 공간의 부분집합)
예시를 들어서 , 설명 해보겠습니다.
실험: 주사위 2개를 던진다.
S: 36개의 결과로 이루어지는집합
A: 사건은 subset이다.
사건 A에대한 확률의 정의
대문자 P(A): 원하는 결과의 가짓수/가능한 결과의수(표본공간의 크기)
실험 : 우리가 동전을 2번 팅귄다 햇을떄
HH,HT,TH,TT
Ex)우리가 두번 모두 뒷면이 나오는 확률을 알고싶다고 한다고 가정하자.
고등학교에서 배운바에 따르면 , 각 확률은 1/4입니다.
분모는 표본공간의 크기와 같고 , 분자의 크기는 가능한 결과의 가짓수가 됩니다.
하지만, 이 동전이 공정한지는 언급하지 않았습니다.
동전이 공정하다는 것은 무슨의미인가??
동전이 공정하다.->앞면과 뒷면이 나오는확률이같다.
예시를 하나더 들어보겠습니다.
ex)내가 해왕성에 생명체가 있을 확률을 발견하고 싶다고 한다.
생명체가 있거나, 없거나 가능한경우는 2가지이다.
그럼 확률은 1/2인가??
터무니없다.
Ex)해왕성에 지능이 있는 생명체가 있을 확률은 어떻게되는가?
있거나, 없거나 , 가능한경우는 2가지.
그럼확률은 1/2인가??? 생명체가 있을 확률 보다 낮아야하는데??
모든 확률에 대해 나올경우가 동등하다면 위에서 정의한 동전이나 주사위에대한 확률적정의는 완벽하다.
이 수업의 첫번쨰 주제는 이 경우들을 어떻게 셀 것인가 입니다.
셈의 기본적인 법칙들을 알아 봅시다.
Multiplication Rule
아시는 분은 skip해주시면 됩니다.
곱의 법칙은 특정한 실험에 적용된다.
만약, 우리가 어떤 실험에서 n1개의 가능한결과가 있다고 하자.
두번쨰 실험에서는 ,첫번 째 실험의 각 결과에대해서 n2개의 가능한결과가 있다고 하자.
총 r번의 실험을 한다.
r번째 실험에서는 r-1번 실험의 결과와 관계없이 nr번의 실험결과가 나온다.
따라서, 전체적으로는 n1,n2,n3…..nr개의 결과가 나온다.
실험 전체에 대해서
실험 전체는 각각의 작은 실험들로 구성된다.
실험 전체는 각각의 작은 실험들로 구성된다.
이 것은귀납법으로 증명할 수잇다.
이것이 정의입니다.
구체적으로 예시를 들어보겠습니다.
ex)Ice Cream
아이스크림을가지고 다양한 실험을 해볼 것이다.
3가지 맛이있고, 콘은 2가지 종류가 있다.
우리는 원하는 맛, 원하는 콘을 고를 수잇다.
첫번쨰 실험은 어떤 형태의 콘을 고를지, 두번쨰 실험은 어떤 맛을 고를지
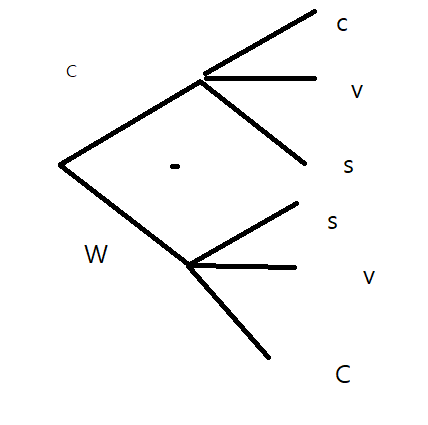
6가지이다.
6= 2* 3 = 3*2
콘을 먼저선택하고 맛을 선택하는것도 되고,
지금은 가짓수가 작지만, 10가지 선택지가 있고 두가지경우중에 선택하는것이라면 1000보다 더많이 나오게 된다.
ex) 포커 풀하우스
이항계수
이항계수 :(n k) = n!/((n-k)!k!)
K 크기를 가지는 부분집합의 개수
n명의 그룹에 대해서 그 순서는 상관없다.
k>n : 0으로 정의
k<n:
k명을 뽑는 경우
첫번째사람:n
두번째 사람:첫번쨰 사람을 제외한 n-1
세번째 사람: n-2
n(n-1)(n-2)…(n-k+1)
여기 가지는 특정한 순서로 사람을 선택할 떄의 경우의 수가 된다.
k명은 어떠한 순서대로 뽑힐수 잇다.
따라서 ,k!로 나누어준다.
풀하우스
풀하우스
Ex)777 10 10 의경우를 생각하자.
분모: (52 5)
분자:
우선 13가지중 하나를 고른다.(우리는 7이라 햇다.)
13
4가지 7중 3개를 고른다.
(4 3)
7을 제외한 12가지중 하나를 고른다.(우리는 10이라 햇다.)
4가지 10중 2개를 고른다.
(4 2)
Sample Table
| 순서를 신경 쓰는가 | 순서를 신경 안쓰는가 | |
| 복원 | n**k | (n-k+1 k) |
| 비복원 | N(n-1)(n-2)…(n-k+1) | (n k) |
표본은 사물이나 사람의 집단을 의미한다.
복원의 의미는 사람을 한명 선택해서 몇가지 질문을 한뒤에 그 사람이 돌아가면 다시 동일한 사람을 선택할 수잇다.
글이 엄청나게 길어진 거 같습니다.
하지만, 초반에 개념을 잘 잡아놓아야 나중에 가서도 개념의 혼동이 오지 않기 때문에 자세하게 적었습니다.
다음 강의도, 계속 올리도록 하겠습니다.
'통계학' 카테고리의 다른 글
| Statistics110 (edwith강의) (0) | 2020.07.18 |
|---|
